Vous est-il déjà arrivé d’entendre dans les conversations cyclistes « mes roues ne sont pas assez rigides, je vais aller les faire retendre » ?

Nous allons chercher à éclaircir ce point souvent discuté qui concerne l’influence des tensions des rayons sur la rigidité latérale de la roue.

Celle-ci dépend de plusieurs paramètres : les matériaux et formes des pièces qui la composent donc la jante, le moyeu, et le rayonnage sur lequel nous allons ici travailler.

La rigidité latérale est un paramètre important pour les performances du coureur.
Faut-il régler la roue avec une tension maximale ? Que ce passe-t-il si la tension est trop faible ?

PROTOCOLE

Le test consiste à appliquer sur une roue une force latérale à l’aide de différentes masses. Durant le test, nous allons relever les valeurs de déplacements au point d’application de la force sur la roue.

Grâce à la masse appliquée et au déplacement de la roue, nous avons converti en N/mm.
Le test s’est déroulé, dans un premier temps, sur une roue route avant car les deux côtés sont symétriques ce qui simplifie les interprétations. Nous étudierons plus tard les roues arrières.

Le point d’application se situe à 90° de la valve, plus précisément au centre de deux rayons. Nous réalisons les mêmes relevés de valeurs à 180° du point d’application. Dans le cas réel, ces valeurs correspondent au déplacement entre les patins de freins.

Nous avons fait varier les tensions de rayons sur une roue puis nous avons observé les effets sur la rigidité latérale de celle-ci.
La tension est homogène sur chacun des rayons de la roue. Les tensions sont données en Newton. Les tests sont effectués entre 1100N et +/-300N. Sous 400N les tensiomètres n’étant plus capables de mesurer avec précision, nous communiquons la valeur de approximative de 300N.

ROUE UTILISEE:
Jante RAR TEMPO 27mm de masse 440g
Moyeu RAR
20 rayons DT Aerolite

 

ANALYSES

Au point d’application de la charge

1. Nous remarquons que les roues ont des déformations très proches peu importe la tension de rayon. En tout cas jusqu’à à un certain seuil à partir duquel les moins tendues perdent leur raideur.

2. Un palier peut être constaté aux alentours de 6000g. La courbe se redresse, signe que la roue a perdu soudainement une bonne part de sa rigidité latérale. Nous supposons que cette perte de rigidité provient du parapluie de la roue, un prochain article sera consacré exclusivement à ce point complexe d’une roue.

3. Nous constatons que pour une tension inférieure à 400N, la roue perd son maintien latéral dès 10kg. Concrètement les rayons du côté où la charge latérale tire ne maintiennent plus la jante et totalement détendus. Seuls les rayons d’un côté de la roue la supporte. Nous allons le vérifier un peu plus tard dans cet article.

4. La roue possédant des rayons tendus à 720N est la plus rigide jusqu’à une masse appliquée de 15kg. Pour des masses supérieures, la roue tendue à 950N est la plus rigide.

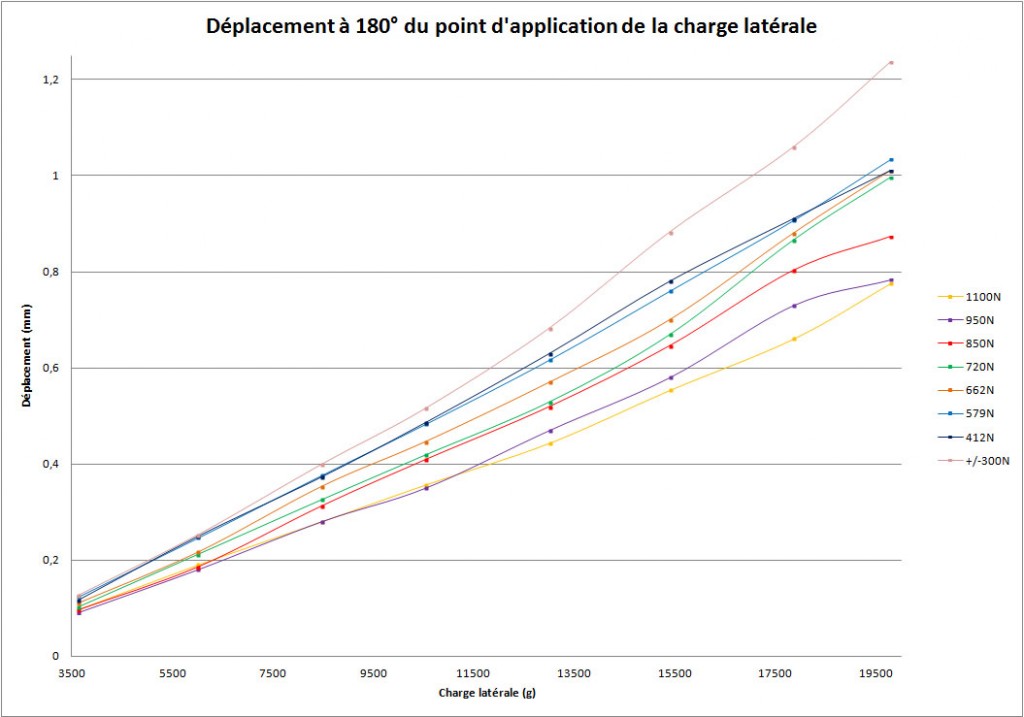
A 180° du point d’application

Nous allons maintenant observer les effets à 180° du point d’application de la force.

1. Au contraire de la valeur de rigidité, nous notons ici des différences plus prononcées entre les essais. A 12000g, la différence entre les deux extrêmes est de 0,25mm environ.

2. Dans ce cas, la hiérarchie des tensions de rayons correspond à celle des déformations: au plus la roue est tendue, au moins elle se déforme.

3. A partir de 10000g, la courbe de la roue à très faibles tensions subit un léger palier: elle change de pente et son déplacement augmente plus rapidement que pour les autres.

4. La roue tendue à 1100N est la moins déformée au-delà de 13500g.

Quid des tensions de rayons autour de la charge?

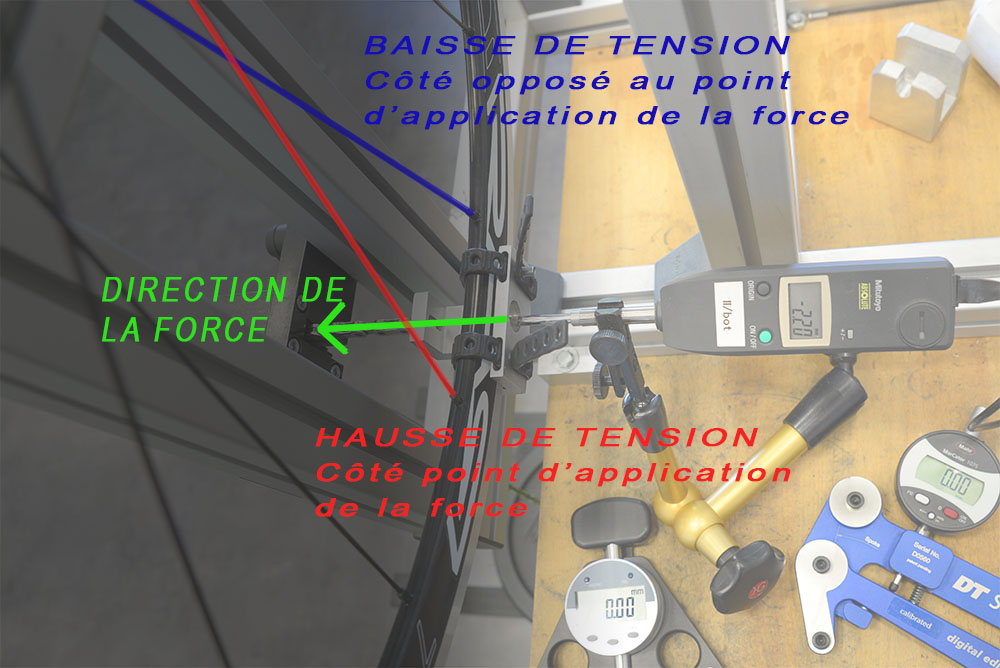
Nous avons cherché à savoir si les tensions de rayons sont modifiées lorsque la charge déforme la roue. Nous chargerons à 10000g, masse la plus représentative des efforts prononcés en danseuse. Cette photo représente ce qui se passe lors du test:

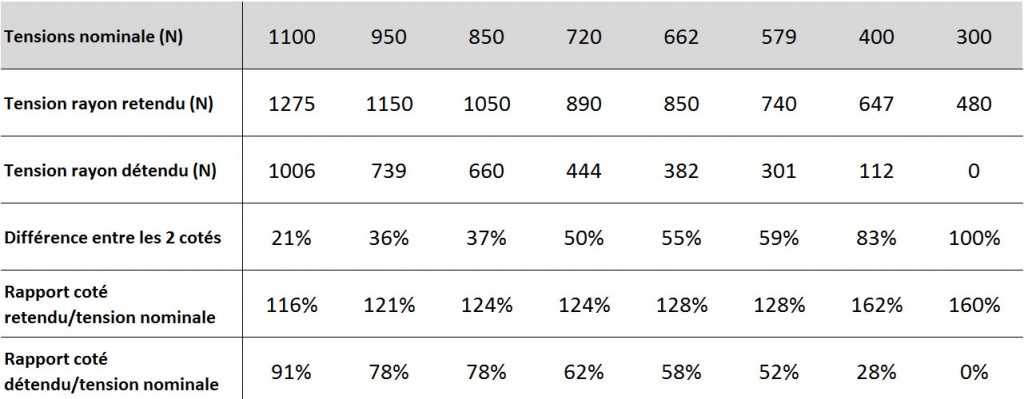
Les tensions enregistrées sont communiquées ci-dessous.

1. Premièrement il est évident que sur une tension très basse, le rayon détendu est alors totalement relâché, il ne contribue plus du tout au maintien latéral de la roue. Ce qui explique la courbe de raideur latérale à 300N en début d’article: un seul côté maintien la roue, au lieu de deux, donc la roue s’affaisse fortement.

2. Deuxièmement, nous constatons qu’au plus les tensions sont élevées, au plus la différence entre le côté qui gagne en tension et celui qui en perd est faible. Ici nous pouvons en conclure que l’influence de la charge latérale devient négligeable sur des tensions de rayons élevées. Ceci explique en partie pourquoi la roue très tendue garde sa rigidité même avec des charges élevées: l’influence de la charge latérale a moins d’impact sur la roue.

Et le pneu dans tout ça?

Les tests ont été réalisés sur une roue non équipée de pneumatique. Lorsque le pneu est en place sur la roue, et gonflé, les résultats évoluent car la pression du pneu influe sur la tension des rayons.
Concrètement les rayons mis sous tension tirent la jante vers le moyeu. Chacun à hauteur de leur tension. La jante supporte donc une force de compression égale au nombre de rayons multiplié par leur tension. Dans notre cas disons 19000N (20×950 environ) soit 1900kg.

Lorsque l’on gonfle la chambre à air du pneumatique, les tringles du pneu viennent tirer sur les crochets de la jante, vers l’extérieur. Ceci applique donc une force inverse à celle des rayons ce qui diminue donc leurs tensions.

En l’occurrence, pour notre roue du test, elle perdra 150N de tension dans chacun des rayons suite à une pression de 7,5 bars dans le pneumatique de section 25mm.
Les résultats du test doivent donc être réinterprétés pour leur contexte. La courbe à 950N se comportera en fonctionnement comme celle à 800N.

FINALEMENT?

Nous pouvons en conclure que la rigidité latérale d’une roue est peu dépendante de la tension des rayons.
Une valeur minimale doit être appliquée pour que la roue soit stable en fonctionnement. De même une valeur maximale ne doit être dépassée : la rigidité latérale est un paramètre parmi beaucoup d’autres dont l’endurance des pièces. Des tensions trop élevées causeront une fatigue accélérée des matériaux.
Nous pouvons également insister sur le fait que la tension des rayons influe sur le déplacement entre les patins de freins : plus la roue est tendue, moins elle bougera dans l’étrier de freins sous les fortes charges latérales, dans les proportions de notre test.

Elargissements.

Avec ce premier article, quelques éclaircissements simples sont apportés sur l’effet des tensions des rayons sur une roue de vélo.
Ensuite, il sera intéressant d’effectuer le même test sur une roue arrière dont les angles de rayonnages jantes/moyeux sont différents de chaque côté.
Il sera intéressant aussi d’élargir les mesures de tensions à des rayons autres que les 2 autour du points d’application de la charge. Finalement, une mesure de déformation à 90° du point de charge pourra s’avérer judicieuse pour les vélos équipés de freins sous le cadre plutôt qu’entre les haubans.